我们如何优化 FLUX.1 Kontext [dev]
【博客转载】我们如何优化 FLUX.1 Kontext [dev]
除了让我们的 FLUX.1 Kontext [dev] 实现开源之外,我们还希望提供更多关于如何在不降低质量的前提下优化它的指导。
在这篇文章中,您将主要了解 TaylorSeer 优化,这是一种通过使用缓存的图像变化(导数)和从 Taylor 级数近似推导出的公式来近似中间图像预测的方法。
各位优化爱好者,请继续阅读。
(我们从以下论文中获取了大部分实现信息:《From Reusing to Forecasting: Accelerating Diffusion Models with TaylorSeers》(从重用到预测:使用 TaylorSeer 加速扩散模型))
如果您前往我们 FLUX.1 Kontext [dev] 代码库中 predict.py 的预测函数,您会找到主要逻辑。(强烈建议通过代码库进行操作,并将此文章作为理解其结构的指南。)
让我们来分解一下。
关于 TaylorSeer
当使用 FLUX.1 Kontext 生成新图像时,您会在多个时间步长中应用扩散变换——连续大约 30 个步骤。在每一步中,一堆变换器层预测对您正在去噪的图像的更新。这个过程可能需要一段时间。
在任何给定的时间步长中,模型预测的变化与之前时间步长的预测具有冗余性。我们可以通过在某些时间步长缓存模型的输出,并在未来的时间步长重用缓存的输出来利用这些冗余性。这种"朴素缓存"——您只是重用最后的特征或潜在值——有时效果还可以,但可能导致模糊、细节丢失,或有时图像完全失真。
您可以尝试稍微聪明一点的方法:线性近似。您可以通过查看最后两步之间的差异(即一阶有限差分)并延长线条来估计下一步。这更好,但仍然不够理想。它无法捕获曲线、加速度或非线性变化——所有这些在扩散模型中都很常见。
TaylorSeer 为此提供了解决方案。它使用 Taylor 级数通过一系列缓存导数来近似模型在时间步长的输出,捕获非线性变化。
用数学术语来说,这是核心思想。为了预测某一层 l 在时间步长 t+k 的特征,我们使用截断的 Taylor 展开:
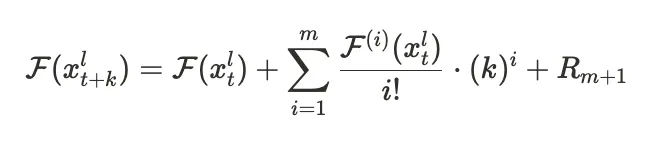
注意,求和需要特征函数的 i 阶导数。由于我们无法计算实际导数,我们可以使用每个 i-1 阶和 i 阶导数之间的有限差分。查看论文了解确切的数学,但当您执行该替换并进行一些简化时,您会得到以下结果:

这是我们对时间步长 t+k 特征的最终近似。
现在我们有了一种通过在特定时间步长使用上述估计来加速扩散过程的方法。
我们设置了一个 TaylorSeer 缓存来在需要时执行此近似:
order = n_derivatives + 1
taylor_seer_state = {
"dY_prev": [None] * order,
"dY_current": [None] * order,
"last_non_approximated_step": 0,
"current_step": 0,
}这里,order = n_derivatives + 1。例如,如果 n_derivatives = 2,那么 order = 3,我们缓存:
dY_current[0]:当前特征dY_current[1]:一阶导数dY_current[2]:二阶导数
denoise() 的前几步总是计算完整预测,用于初始化有限差分。后面的步骤可以近似。
逐步解析:TaylorSeer 在 Flux Kontext 中的工作原理
一旦我们准备好输入,我们使用 generate_compute_step_map() 决定哪些步骤要计算,哪些要近似:
def generate_compute_step_map(acceleration_level: str, num_inference_steps: int):
if acceleration_level == "none":
return [True] * num_inference_steps
elif acceleration_level == "go fast":
# 计算前 4 步和后 4 步,中间所有步骤交替进行
k = [False, True]
compute_step_map = [k[i % 2] for i in range(num_inference_steps)]
compute_step_map[:4] = [True] * 4
compute_step_map[-4:] = [True] * 4
return compute_step_map
elif acceleration_level == "go really fast":
# 计算前 3 步和后 3 步,中间所有步骤在完整计算一次和近似两次之间交替
k = [False, True, False]
compute_step_map = [k[i % 3] for i in range(num_inference_steps)]
compute_step_map[:3] = [True] * 3
compute_step_map[-3:] = [True] * 3
return compute_step_map
....generate_compute_step_map() 遵循一个简单规则:始终计算前几步和后几步,因为这是模型做出最大变化的地方。在中间步骤中,我们在"快速"模式下每隔一步计算一次,或在"非常快速"模式下每隔三步计算一次。像 First Block Cache 这样的自适应方法,检查第一个变换器块输出的变化程度,可能是确定要跳过哪些步骤的明智做法,但这种硬编码策略效果很好。
两条路径:计算或近似
在去噪循环中:
if compute_step_map[current_step]:
pred = model(...) # 完整预测
taylor_seer_state['dY_current'] = approximate_derivative(...)
else:
pred = approximate_value(...) # 使用 TaylorSeer 预测让我们分解每条路径。
路径 1:完整计算
我们正常运行模型并更新我们存储的有限差分(导数):
dY_current[i+1] = (dY_current[i] - dY_prev[i]) / finite_difference_window
这是从低阶有限差分递归计算高阶有限差分的视图。第 m+1 阶导数来自第 m 阶导数值在经过时间内的差异。
这些差异近似特征值如何随时间演变。
路径 2:使用 Taylor 级数近似
如果我们决定跳过一步(基于 compute_step_map),我们使用缓存的差分来估计下一个特征更新(来自方程 2 的近似):
output += (1 / math.factorial(i)) * dY_current[i] * (elapsed_steps ** i)
计算此近似所需的时间与运行完整模型进行单次去噪步骤所需的时间相比几乎是瞬时的。
更新潜在变量
在每一步中,无论我们是计算还是近似,我们都将预测的增量应用到图像潜在变量:
img = img + (t_prev - t_curr) * pred
这使图像变换在时间步长中持续演进。
去噪循环结束后,我们返回最终图像!
总结
我们不再在每个时间步长评估模型,而是:
- 缓存过去的预测及其有限差分。
- 使用 Taylor 级数近似模型在跳过步骤的输出。
- 减少模型调用从 30 次到大约 10-15 次,取决于速度设置。
- 保持质量,特别是在生成的开始和结束阶段,那里准确性最重要。
TaylorSeer 为我们提供了一种有原则、灵活的方式,使用特征动力学来预测图像生成中的中间步骤。它比运行每一步都更快,比线性外推更智能。
您可以在我们的 FLUX.1 Kontext 代码库中的 denoise() 和 taylor_utils.py 中找到所有这些内容。
尽情探索代码库,告诉我们您的发现!
试一试: FLUX.1 Kontext [dev]