Diffusion Models 可视化逐步入门
Diffusion Models 可视化逐步入门
本文为原文《Step by Step visual introduction to Diffusion Models》的中文翻译,原作者 Kemal Erdem。
什么是扩散模型?
扩散模型的概念并不久远。2015 年的论文《Deep Unsupervised Learning using Nonequilibrium Thermodynamics》中,作者这样描述:
其核心思想,受非平衡统计物理学启发,是通过逐步的前向扩散过程系统性地、缓慢地破坏数据分布中的结构。随后我们学习一个反向扩散过程,恢复数据结构,从而获得对数据高度灵活且易于处理的生成模型。
这里的扩散过程分为前向和反向两个阶段。前向扩散过程是将一张图片变成噪声,反向扩散过程则试图将噪声还原为图片。
前向扩散过程
如果上面的定义还不够清楚,别担心,我们可以解释其原理和实现方式。首先,你需要知道如何破坏数据分布中的结构。


图 1:前向扩散过程的输入与输出
如果我们取任意一张图片(如图 1a),它有某种非随机分布。我们虽然不知道具体分布,但目标是通过加噪声来破坏它。最终应得到类似纯噪声的结果。
图 2:仅用 10 步的前向扩散过程
每一步的前向扩散过程定义为:
$$ q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I) $$
其中 $q$ 是前向过程,$x_t$ 是第 $t$ 步的输出,$x_{t-1}$ 是输入,$\mathcal{N}$ 表示正态分布,$\sqrt{1-\beta_t}x_{t-1}$ 是均值,$\beta_t I$ 是方差。
调度表(Schedule)
$\beta_t$ 称为“调度表”,取值范围通常在 $0$ 到 $1$ 之间。2020 年的论文[2]使用线性调度:

图 3:使用 1000 步线性调度的前向扩散过程
此时 $\beta_t$ 从 0.0001 到 0.02,均值和方差变化如图 4 所示。
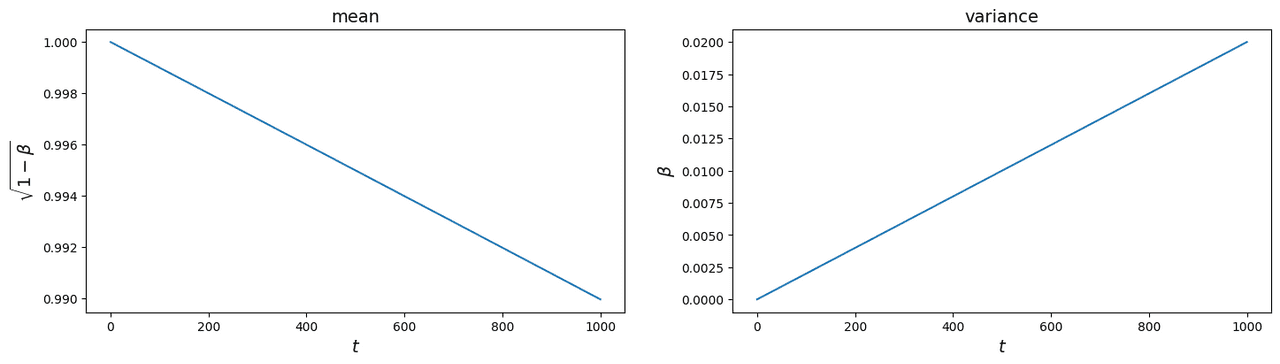
图 4:不同步长下均值和方差的变化
OpenAI 2021 年的论文[3]认为线性调度效率不高。正如你所见,原图大部分信息在一半步数后就丢失了。他们设计了自己的“余弦调度”(cosine schedule,见图 5),使步数减少到 50。

图 5:使用余弦调度的前向扩散过程
实际加噪过程(只需关注最后一个公式)
你可以想象,前向扩散过程加噪会很慢。训练时并不是严格按顺序采样,而是直接从任意 $t$ 采样。2020 年论文提出:
$$ q(x_{1:T}|x_0) := \prod_{t=1}^{T} q(x_t|x_{t-1}) $$
这个过程可以看作函数复合:
$$ q_t(q_{t-1}(q_{t-2}(\cdots q_1(x_0)))) $$
$t=1$ 时:
$$ q(x_1|x_0) = \mathcal{N}(x_1; \sqrt{1-\beta_1}x_0, \beta_1 I) $$
$t=2$ 时:
$$ q(x_2|x_1) = \mathcal{N}(x_2; \sqrt{1-\beta_2}x_1, \beta_2 I) $$
引入记号:
- $\alpha_t = 1 - \beta_t$
- $\bar\alpha_t := \prod_{s=1}^t \alpha_s$
则有:
$$ q(x_1|x_0) = \mathcal{N}(x_1; \sqrt{\alpha_1}x_0, (1-\alpha_1)I) $$
均值递推:
$$ \mu_t = \sqrt{\bar\alpha_t}x_0 $$
最终整体公式:
$$ q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)I) $$
单步重参数化:
$$ q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I) = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon $$
其中 $\epsilon \sim \mathcal{N}(0, 1)$。
反向扩散过程
你可能已经猜到,反向扩散过程的目标是将纯噪声还原为图片。为此,我们会用到神经网络(暂不讨论架构,后文会详细介绍)。如果你熟悉 GAN(生成对抗网络,见图 6),我们要训练的类似于生成器网络。不同之处在于,我们的网络每次只需做一小步,任务更轻松。
图 6:GAN 架构
那么为什么不用 GAN 呢?许多聪明人花了很长时间才让 GAN 取得不错的效果。要让网络直接把随机噪声变成有意义的图片,训练极其困难。2015 年的论文[1]作者发现,采用多步框架、每次只去除一部分噪声,更高效也更易训练。
在这个框架下,学习的本质是估计扩散过程中的微小扰动。估计小扰动比用单一、不可解析归一化的势函数描述完整分布更易处理。此外,只要目标分布是光滑的,扩散过程总能拟合任意形式的数据分布。
关于反向扩散的误解
你可能听说过“扩散概率模型是参数化马尔可夫链”。这没错,但很多人误解了扩散模型中的神经网络作用。2020 年论文[2]用下图描述了过程:
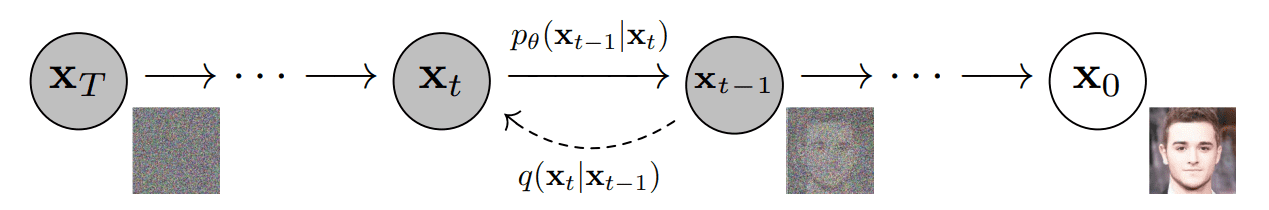
图 7:有向图模型
通常神经网络被这样可视化:
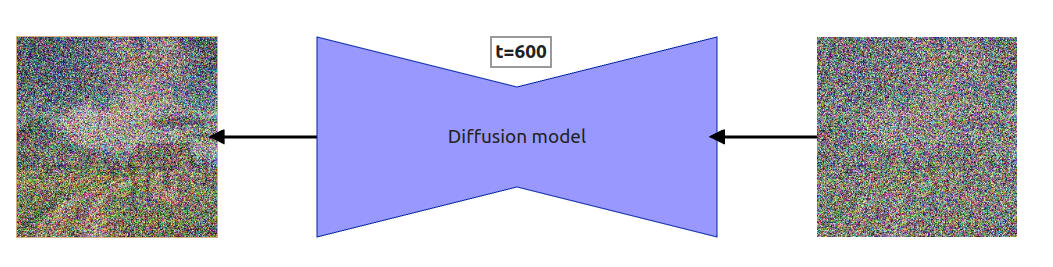
图 8:反向扩散单步高层可视化
因此,很多人以为神经网络(也叫 diffusion model)是在去除输入图片的噪声,或预测要去除的噪声。其实都不对。扩散模型预测的是在给定步长下需要去除的全部噪声。比如步长 $t=600$,模型预测的是去除全部噪声后应还原到 $t=0$,而不是 $t=599$。后文会详细解释,先看反向扩散的逐步过程。
注意:我把步数从 1000 缩减到 10,是为了让人类更容易比较每一步的结果。
图 9:反向扩散过程
一些数学推导(可跳过,但值得一读)
过程看似简单,但你可能会问“这些输出公式从哪来的?”我们先引用 2020 年论文[2]的反向过程公式:
$$ p_\theta(x_{0:T}) := p(x_T) \prod_{t=1}^{T} p_\theta(x_{t-1}|x_t) $$
其中:
$$ p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t,t), \Sigma_\theta(x_t,t)) $$
这其实就是:扩散过程 $p_\theta(x_{0:T})$ 是一串高斯转移链,从 $p(x_T)$ 开始,迭代 $T$ 次,每次用 $p_\theta(x_{t-1}|x_t)$。
单步公式有两部分:
- $\mu_\theta(x_t,t)$(均值)
- $\Sigma_\theta(x_t,t)$,等于 $\sigma_t^2 I$(方差)
2020 年论文设定方差为随时间变化但不可训练,即 $\beta_T I$,与前文调度表一致。只剩均值部分。更详细的数学推导可参考 Lilian Weng 的博客[6] 或论文附录。
我们只需知道:
$$ \mu_\theta(x_t,t) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}} \epsilon_\theta(x_t, t) \right) $$
因此:
$$ x_{t-1} = \mathcal{N}\left(x_{t-1}, \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}} \epsilon_\theta(x_t, t)), \sqrt{\beta_t}\epsilon\right) $$
可用于计算任意步长 $t$ 的输出:
$$ x_{t-1} = \frac{1}{\sqrt{a_t}} \left(x_t - \frac{\beta_t}{\sqrt{1-\bar\alpha}} \epsilon_\theta(x_t,t)\right) + \sqrt{\beta_t}\epsilon $$
其中 $\epsilon_\theta(x_t,t)$ 是模型输出(预测噪声)。
如图 9,最后一步不再加 $\sqrt{\beta_t}\epsilon$,否则无法去除。
反向扩散输出可视化
在介绍架构前,先展示一个有趣的现象。每次神经网络预测噪声后,我们减去一部分并进入下一步,这就是扩散过程。但**如果每步都减去全部噪声会怎样?**我用线性调度(1~50 步)做了实验:
注意!反向过程下,$t=1$ 时 $\beta_t$ 实际为 $\beta_{T-t+1}$,即 $t=1$ 用 $\beta_{50}$,$t=2$ 用 $\beta_{49}$,以此类推。

图 10:全部噪声移除的结果
中间是第 $t$ 步输入,$t=0$ 时为纯噪声。右侧是神经网络预测的噪声,左侧是每步输入减去全部噪声的结果。只展示部分步长,完整过程见 gDrive。
如文首所述,扩散模型本质上类似 GAN 的生成器,但单步去噪效果更差。你会发现,第一步移除全部噪声的结果与最终生成图像很接近。这是因为我们训练模型预测的是全部噪声,而不是差分。理论上完美模型应能预测出能还原正确图片的全部噪声,但这几乎不可能。
你可以得出两点:
- 推理时可用更少步长
- 推理时可用不同调度表
第一点很直观,模型预测的噪声已很接近目标时,可以“跳步”。第二点则是可以用不同斜率的调度表(如训练用线性,推理用余弦)。
架构
最后我们来讨论模型架构。
喜欢看 PyTorch 可视化的同学可参考 完整模型结构(gDrive)。
图 11:Diffusion model 架构
模型采用改进版 U-Net[7],基础结构简单,后续如 Stable Diffusion 等会加入更多特性(如潜空间编码)。本文只讲最基础版本,理解后可举一反三。
Embeddings
每一步都要输入步长和 prompt 信息。实际上,每步都要加上步长和 prompt 的 embedding(最早的 diffusion model 不支持 prompt)。步长用正弦位置编码,prompt 用嵌入器。相关原理可参考transformer 位置编码。
嵌入器
嵌入器可以是任意网络。最早的条件扩散模型(支持 prompt)用的很简单,比如本文实验用的 CIFAR-10 数据集只有 10 类,嵌入器只需编码类别。如果数据集更复杂,或无标注,可用如 CLIP 之类的嵌入器,训练时也要用同样的嵌入器。
位置编码和文本嵌入输出相加后,输入到下采样和上采样模块。
ResNet Block
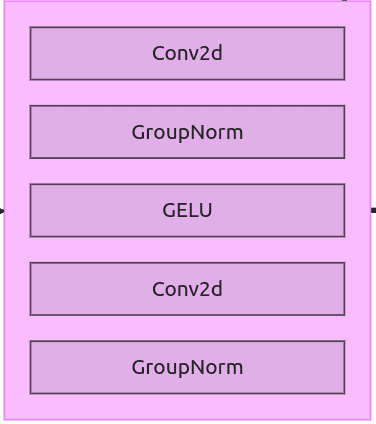
图 12:ResNet block
ResNet block 结构简单,后续会作为下采样和上采样模块的组成部分。
Downsample Block
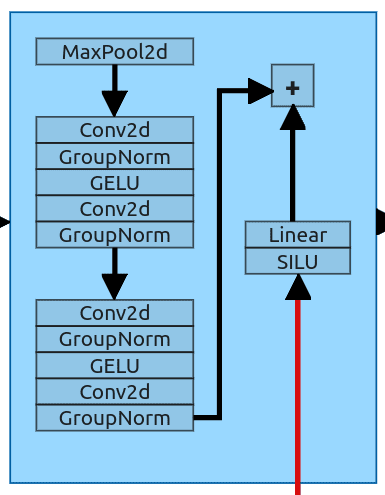
图 13:Downsample block
Downsample block 首先接收前一层输出和步长、prompt 信息。它用 MaxPool2d 层(核为 2)将输入尺寸减半(64x64 -> 32x32),然后通过 2 个 ResNet block。
嵌入信息经过 SILU 和线性层处理后,与 ResNet block 输出相加,再送入下一个模块。
Self-Attention Block
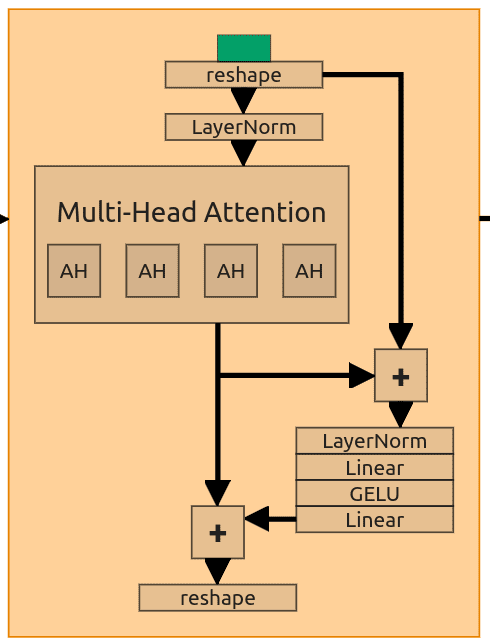
图 14:Self-Attention block
部分 ResNet block 被 Attention block 替换。Attention block 结构一致,这里以第一个为例。输入为 (128, 32, 32),经过多头注意力(128 维,4 头),嵌入维度会变化,头数不变。
输入需 reshape,最后两维合并并转置,(128,32,32) -> (128,1024) -> (1024,128)。LayerNorm 后作为 Q、K、V。
内部有 2 个 skip connection,分别加到 attention 层输出和后续前馈层输出上。最后再 reshape 回原形状。
Upsample block
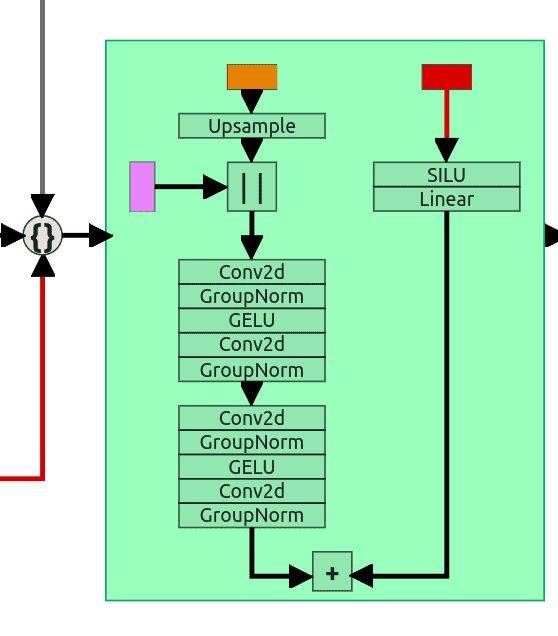
图 15:Upsample block
Upsample block 有 3 个输入。主输入经过上采样(scale=2),与残差连接拼接,形状统一后通过 2 个 ResNet block。第三个输入(步长和 prompt 嵌入)同样处理后加到第二个 ResNet block 输出。
最后用 1x1 卷积将输出通道数变回 (3,64,64),即为预测噪声。
训练
训练过程非常简单,伪代码如下:
1: repeat
2: $x_0 \sim q(x_0)$
3: $t \sim \mathrm{Uniform}({1,\ldots,T})$
4: $\epsilon \sim \mathcal{N}(0,I)$
5: 梯度下降 $\nabla_\theta | \epsilon - \epsilon_\theta(\sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t} \epsilon, t) |^2$
6: 直到收敛
每次从数据集中采样图片(2),采样步长 $t$(3),采样噪声(4)。如前文所述,无需逐步加噪,直接用:
$$ q(x_t|x_0) = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}\epsilon $$
优化目标即为(5),重复直到收敛。
总结
本文较长,但希望你能读懂。这里只介绍了早期扩散模型,未涉及 CFG、负向提示、LORA、ControlNet 等后续进展,后续会单独介绍。你需要记住:
- 扩散过程包括前向扩散和反向扩散
- 前向扩散通过调度表加噪
- 调度表有多种(如线性、余弦),决定每步加多少噪声
- 加噪可一步完成,无需迭代
- 反向扩散多步去噪,每步去除一小部分噪声
- 扩散模型预测的是全部噪声,不是相邻两步的差分
- 推理时可用不同调度表和步数
- 模型结构为改进版 U-Net
- 步长和 prompt 信息通过正弦编码和嵌入器输入
- 部分 ResNet block 被 Self-Attention block 替换
参考文献
- Deep Unsupervised Learning using Nonequilibrium Thermodynamics(论文)
- Denoising Diffusion Probabilistic Models(论文)
- Improved Denoising Diffusion Probabilistic Models(论文)
- Diffusion Models Beat GANs on Image Synthesis(论文)
- Classifier-Free Diffusion Guidance(论文)
- What are diffusion models?(博客)
- U-Net: Convolutional Networks for Biomedical Image Segmentation(论文)
- Learning Transferable Visual Models From Natural Language Supervision(论文)
引用
Kemal Erdem, (Nov 2023). "Step by Step visual introduction to Diffusion Models.". https://erdem.pl/2023/11/step-by-step-visual-introduction-to-diffusion-models
或
@article{erdem2023stepByStepVisualIntroductionToDiffusionModels,
title = "Step by Step visual introduction to Diffusion Models.",
author = "Kemal Erdem",
journal = "https://erdem.pl",
year = "2023",
month = "Nov",
url = "https://erdem.pl/2023/11/step-by-step-visual-introduction-to-diffusion-models"
}ML Developer, Software Architect, JS Engineer, Ultra-distance cyclist
Kemal Erdem on Twitter: https://www.twitter.com/burnpiro